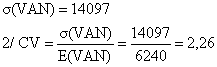UNIVERSITÉ DE SFAX
École Supérieure de Commerce
Enseignant : Walid KHOUFI
1. Introduction
D’après le chapitre précédent, l’étude financière des
projets d’investissement consiste à analyser leur rentabilité en supposant que les flux monétaires sont connus avec
certitude, mais cette hypothèse n’est pas une description exacte de la réalité.
En effet les flux monétaires utilisés ne sont que des prévisions qui sont
susceptibles de varier substantiellement dans le temps. Dans ces conditions,
l’analyse de la rentabilité d’un projet d’investissement devra incorporer le
facteur risque.
2. Les méthodes approximatives pour tenir compte du risque d’un projet :
Ces
méthodes consistent à ajuster la valeur actuelle nette VAN du projet pour tenir
compte de son risque.
L’ajustement
de la VAN s’effectue en modifiant l’un des paramètres suivants :
- La
durée du projet,
- Les
flux monétaires,
- Le
taux d’actualisation,
Les corrections apportées à ces paramètres sont dans la plupart des cas, purement subjectives et
dépendent du degré d’aversion des gestionnaires envers le risque.
2.1. Réduction de la durée du projet
En se basant sur le fait que
les flux monétaires les plus éloignés dans le temps sont les plus risqués,
certains praticiens considèrent qu’un raccourcissement de la durée de vie
permet dès lors d’annuler le risque attaché au projet. Ainsi, plus un projet sera jugé risqué
par les gestionnaires, plus grand sera
le nombre d’années qui sera retranché de sa durée de vie initialement prévue.
Le
calcul de la VAN s’effectue alors comme suit :
Où n = durée de vie initialement prévue pour le projet.
x = nombre d’années à retranchés pour
tenir compte du risque
du projet.
E(CFNt)
= cash-flow net espéré pour la période t .
Io : investissement
initial.
i :
taux d’actualisation approprié pour les flux monétaires.
Remarque : le taux
d’actualisation utilisé est le taux sans risque étant donné que l’on tient
compte du risque en réduisant un certain nombre d’années de la durée de vie
initiale du projet.
Exemple 1
|
|
|
|
Une
entreprise a la possibilité d’investir dans
projet dont les caractéristiques sont les suivantes : Investissement
= 100000 TND Taux
sans risque = 10 % Durée
de vie = 15 ans Cash-flow
net annuel = 15000 TND Compte
tenu du risque du projet l’un des dirigeants désire retrancher les quatre
dernières années de la durée de vie normale du projet alors qu’un autre
dirigeant estime qu’une pénalité de trois ans serait suffisante. Déterminer
la VAN du projet selon chacune de ces deux hypothèses.
|
Solution
|
-
Pénalité de 4 ans : - Pénalité de 3 ans :
A travers cet exemple nous remarquons que dans un
cas le projet est non rentable, alors que dans l’autre nous pouvons
l’accepter. Cette démarche est très arbitraire puisque la pénalité attribuée
au projet est purement intuitive et dépend de l’attitude de l’analyste envers
le risque.
|
Cette approche est très arbitraire et a tendance à
pénaliser les projets dont les flux monétaires les plus importants se situent au
niveau des dernières années. Sur le plan théorique, il est difficile de
recommander l’utilisation de cette méthode pour tenir compte du risque.
2.2.
Méthodes basée sur l’ajustement des flux monétaires
Cette approche, connue également sous le nom de
la méthode de l’équivalent certain, consiste à pénaliser la VAN en transformant
les cash-flows nets espérés du projet en montants certains par le biais d’une
série de coefficients d’ajustement (
).
Ces coefficients ont des valeurs comprises entre 0 et 1 et varient de
façon inverse avec le degré de risque des cash-flows.
Pour calculer la VAN nous employons la formule suivante :
Avec 
: coefficient d’ajustement du cash-flow pour la
période t.
i : taux
d’actualisation sans risque (Voir remarque du paragraphe précédent).
Exemple 2
|
|
|
|
Soit
un projet d’une durée de vie égale à 2 ans et
nécessitant un investissement de 1000 TND. Le cash-flow espéré de la
première année est 400 TND alors que celui de la deuxième année est de 1100
TND. On
suppose que le taux des bons de trésor pour une échéance de 2 ans est de 10%
et que le gestionnaire du projet attribue aux différents flux
monétaires les coefficients d’ajustement suivant: 1/
Doit-on accepter ce projet? 2/ Calculer la pénalité attribuée à ce projet pour tenir compte du risque.
|
Solution
|
1/ La
VAN est supérieure à 0, donc le projet est à accepter. 2/VAN’= VAN du projet en ignorant le facteur risque
La
différence entre les deux VAN obtenues égale à 272,727 – 54,545 = 218,182 TND
représente la pénalité attribuée au projet pour tenir compte du fait que le
flux monétaires sont risqués.
|
; 
Il reste à signaler que les applications pratiques de cette
méthode sont limitées compte tenu de la difficulté à déterminer les valeurs à
attribuer aux coefficients d’ajustement.
2.3.
La méthode du taux d’actualisation ajusté
Se basant sur le fait que le
rendement exigé sur un investissement doit être lié au niveau de risque
encouru, certains considèrent que la pénalisation de la VAN pour tenir compte
du risque peut se faire en ajustant le taux d’actualisation en fonction du
degré de risque du projet. Ainsi pour déterminer le taux à utiliser pour
actualiser les flux monétaires incertains, on ajoutera au taux sans risque une
certaine prime qui tient compte du risque.
Ainsi le
taux d’actualisations ajusté k se calcule de la façon suivante:
k = taux sans risque + prime pour le
risque.
k = i + r
Où
k = taux d’actualisation ajusté.
i = taux sans risque
r = prime
pour le risque normal de l’entreprise et pour le risque spécifique lié au
projet.
Ainsi 
3. Les méthodes
de mesure du risque d’un projet
Il s’agit
des méthodes qui utilisent les distributions de probabilité des flux monétaires
pour évaluer le risque spécifique d’un projet. La mesure utilisée est l’écart type
qui représente la dispersion des VAN possibles par rapport à la VAN espérée ou
moyenne. En d’autres termes il représente la volatilité de la VAN.
3.1. Cas des projets d’une seule période
La valeur actuelle nette d’un projet se calcule
ainsi :
n : nombre
d’événements possibles associés au projet
Pj :
probabilité de réalisation du jième événement
VANj : Valeur
actuelle nette du projet si le jième
événement se produit.
Alors que la variance de la VAN se calcule
à l’aide de l’expression :
Quant à l’écart type qui caractérise le risque
inhérent à un projet est égale à :
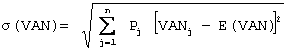
Plus l’écart
type est élevé, plus les VAN possibles ont tendance à différer de la VAN espérée
donc plus le risque du projet, est grand.
Lorsque nous comparons plusieurs
projets de VAN espérées différentes mais de risques égaux nous retiendrons le
projet ayant la VAN espérée la plus élevée. Mais lorsque nous comparons
plusieurs projets de VAN espérées égales et de risques
différents nous choisirons le projet ayant le risque (s(VAN))
le plus faible. Enfin si nous comparons des projets de VAN espérées différentes
et de risques différents, la solution à retenir dépendra du degré d’aversion du
gestionnaire envers le risque. Cependant, pour faciliter la prise de décision,
certains analystes calcule le degré de risque par unité de rendement espéré du
projet représenté l’équation suivante connue sous le nom du coefficient de
variation :
Exemple 3
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Considérons
deux projets mutuellement exclusifs X et Y. Chacun des deux projets a une
durée de vie d’un an et permet la réalisation des cash-flows suivants : Projet X:
Investissement 50000 TND
Projet Y: Investissement
30000 TND
Le taux
sans risque est de 10% A/ Calculer pour chacun des projets la VAN
espérée et son risque B/ Quel projet la firme devrait-elle retenir si son
objectif est de minimiser le coefficient de variation. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Solution
|
Projet X 1-
Calcule de la VAN espérée
2-
Calcul du risque s²( s²( d’où s ( Projet Y 1-
Calcul de la VAN espérée
s²(
0,3(24545,455–6363,636) s²( d’où s( Calcul
des coefficients de variation
Compte tenu de son objectif, l’entreprise devrait retenir
le projet X puisqu’il offre le plus faible risque relatif. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
)
) =
+ 0,2(
)
3.2. Projet
dont les flux monétaires s’étalent sur plusieurs périodes
Lorsque la durée des projets couvre
plusieurs périodes, il est nécessaire, en premier lieu, d’identifier la nature de
la dépendance existant entre les flux monétaires successifs. La relation entre
ces derniers peut être de trois types: indépendance totale, dépendance totale
ou dépendance partielle.
3.2.1. Indépendance
des flux monétaires dans le temps
Il y a indépendance entre les flux
monétaires d’un projet si les flux monétaires d’une période quelconque ne sont
aucunement affectés par ceux des périodes précédentes et n’affectent pas ceux
des périodes subséquentes.
Dans ce contexte d’indépendance, la
VAN espérée d’un projet se calcul de la manière suivante :
E(VAN) = 
Pour le calcul du risque, la formule à utiliser
est la suivante :
s(VAN)=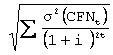 
Exemple 4
|
|
||||||||||||||||||||||||
|
|
Soit un projet d’une durée de vie de
2 ans, nécessitant un investissement de 50000 TND et dont la distribution de
probabilité relative aux flux monétaires a la configuration suivante:
On suppose que les flux sont
complètement indépendants entre eux et que le
taux sans risque est de 10%. A/ Calculer
la valeur actuelle nette espérée du projet et le risque de ce dernier. B/ Ce projet devrait-il être accepté ?
|
||||||||||||||||||||||||
Solution
|
E( E( E(VAN) = 909,091
Le choix ou le rejet du projet dépend du degré
d’aversion du gestionnaire envers le risque. Pour faciliter la prise décision, il peut être utile
de calculer la probabilité que la VAN du projet soit négative, et ce en
supposant une distribution normale et en ayant recours à la table de la loi
normale.
=
=
=
= 1- = 0 Comme la possibilité d’avoir une
VAN négative est nulle le projet sera fort probable accepté. Remarque : le problème peut également être résolu en utilisant l’arbre de décision que nous présenterons dans le paragraphe 3.2.3.
|
||||||||||||||||||||||||
) = 31000 
) = 27500
(
3.2.2. Dépendance totale des flux monétaires dans
le temps.
Dans le contexte de dépendance totale
des flux monétaires dans le temps, les flux monétaires de la période t
dépendent entièrement des résultats obtenus au cours des périodes précédentes.
Dans une telle situation, la formule donnant la VAN espérée du projet
n’est pas affectée par cette modification d’hypothèse.
Alors que le risque du projet
s’évalue ainsi :
Exemple 5
|
|
|
|
Reprenons l’exemple précédent mais en supposant que les
flux monétaires sont totalement dépendants entre eux. |
Solution
|
on
remarque que le risque du projet est plus élevé lorsque les flux monétaires
sont parfaitement et positivement corrélés que dans une situation ou ils sont
indépendants
|
3.2.3 Dépendance
partielles des flux monétaires dans le temps.
Dans la
plupart des situations rencontrées en pratique, les flux monétaires d’un projet
sont d’un point de vue statistique positivement mais imparfaitement corrélés. Pour
aborder ce problème, il faut introduire une série de distribution de
probabilités conditionnelles.
Exemple 6 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Soit un projet nécessitant un investissement de
50000 TND et dont la durée est de deux ans. Le taux sans risque est de 10% et
les flux monétaires ont la configuration suivante:
1/ Déterminer la VAN espérée et le risque du projet 2/ Les dirigeants de l’entreprise ont décidé de n’accepter
que les projets ayant un coefficient
de variation inférieur où égal à 0,9
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Solution |
1ère méthode :
2e méthode :
En se basant sur la règle de décision établie par
les gestionnaires, ce projet ne devrait pas être retenu.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. L’évaluation du risque d’un projet en contexte
de portefeuille
Les différentes méthodes examinées jusqu’à maintenant
ont permis de porter un jugement sur la rentabilité et le risque d’un projet
pris isolement. Toutefois, étant donné que l’objectif des gestionnaires est la
maximisation de la valeur de l’entreprise,
et sachant que cette dernière est fonction de la valeur des projets
d’investissement de l’entreprise considérés dans leur ensemble, il apparaît
plus judicieux d’évaluer le risque global de l’entreprise en considérant
l’impact du risque relatif au nouveau projet. Dès lors, il convient de
remarquer qu’entre deux projets, le meilleur projet, pris isolement, n’est pas
nécessairement le meilleur si l’on prend en considération tous les projets
de l’entreprise (nouveaux et anciens). La démarche à suivre à ce niveau est
inspirée de la théorie de portefeuille.
Considérons un portefeuille p constitué de projets
d’investissement, la valeur actuelle nette de ce portefeuille (p) est égale à
la somme des valeurs actuelles nettes de chacun des projets
(1,2,…,n)constituant le portefeuille :
E(VANp)= E(VAN1) + E(VAN2)
+…….+ E(VANn).
Alors que la variance du portefeuille est obtenue en
additionnant la variance de chacun des n projets et les variances de chaque
paire de projets. Algébriquement nous avons :
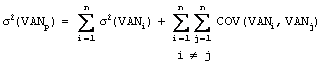
Puisque 
l’expression s’écrit également :
Le degré de dépendance linéaire existant entre
la VAN de deux projets se mesure au moyen du coefficient de corrélation qui se
calcul ainsi :
Ce coefficient de corrélation peut varier entre 1 et –1 :
Si 
: les projets évoluent exactement dans la même
direction. On dit qu’ils sont positivement et parfaitement corrélés.
Si 
: les projets
évoluent exactement en directions opposées. On dit qu’ils sont négativement et
parfaitement corrélés.
Si 
Les projets
évoluent indépendamment les des autres.
Remarque :
Généralement, en pratique, la plupart des projets retenus par une entreprise
sont corrélés positivement, mais
imparfaitement.
Il faut également remarquer que lorsque la
covariance entre les VAN des projets n’est pas connue directement, on peut
l’évaluer en utilisant l’égalité suivante:
où
: probabilité de
réalisation de la conjoncture k.
: VAN du
projet i étant donné la conjoncture k.
: VAN du
projet j étant donné la conjoncture.
Exemple 7
|
|
||||||||||||||||||||||||||
|
|
L’entreprise AZF étudie la
possibilité d’entreprendre l’un des deux projets mutuellement exclusifs X et
Y dont les caractéristiques figurent dans le tableau suivant : Nouveaux
projets à l’étude : X et Y
Les projets actuellement en cours dans
l’entreprise ont les caractéristiques suivantes : Projets
actuellement en cours dans l’entreprise
Quel projet AZF a intérêt de choisir ? |
||||||||||||||||||||||||||
Solution
|
Considérant d’abord chacun des
projets isolément : * Projet X
* Projet Y
Résumé :
Voyons maintenant l’impact de
chacun des projets sur le risque global de l’entreprise.
* Projets actuellement en cours dans l’entreprise
* Première combinaison
E+X :
* Deuxième combinaison
E+Y :
Résumé :
|
||||||||||||||||||||||||||
5. L’analyse des projets d’investissement et
le CAPM ou le MEDAF
L’analyse des projets
d’investissement, en utilisant le MEDAF, permet de déterminer le taux
d’actualisation approprié pour un projet d’investissement c’est-à-dire le taux de
rendement minimal à exiger sur un projet d’investissement.
En effet, du point de vue d’un investisseur
détenant un portefeuille de titres largement diversifié, le rendement minimal à
exiger sur un projet d’investissement devrait être lié à son risque systématique
de la façon suivante :
Où
K : taux de rendement minimal
acceptable sur le projet d’investissement .
r : taux
de rendement l’actif sans risque
taux de rendement espérée du marché
coefficient bêta du projet = risque systématique =
Pour déterminer si un projet donné
doit être accepté ou non, il convient de comparer le taux de rendement minimal (K)
qu’exigerait le marché sur ce projet compte tenu de son risque avec le taux de
rendement interne espéré du projet. Si le taux de rendement interne espéré du
projet excède le taux de rendement exigé par le marché, le projet devrait être
accepté, si non il devrait être rejeté.
Remarque :
* Ce modèle ne devrait être utilisé que pour des projets dont la durée
de vie est d’une seule période car l’une des hypothèses de base du MEDAF est
que l’horizon de planification est d’une période.
* En outre, l’équation ne devrait
être utilisée pour déterminer le taux de rendement minimal à exiger sur un
projet d’investissement que dans les deux cas suivants :
1- l’entreprise est financée à 100% par des fonds
propres ou
2- la structure de capital n’a aucune influence sur le coût du capital.
Si cette ces conditions ne sont pas vérifier il convient d’ajuster le taux de rendement minimal pour tenir compte de l’impact du financement par dette.